Hot Right Now
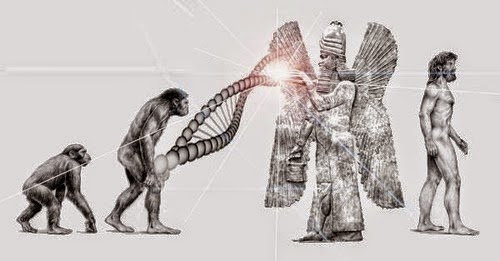
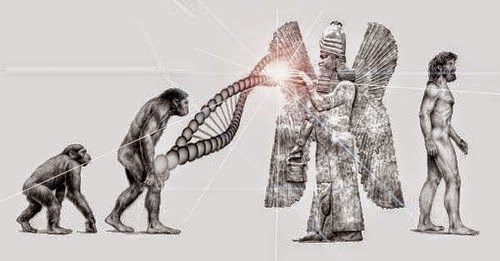
Ancient Sumerian Texts: Ancient Clay Tablets reveal secrets about Alien life
Among the many ancient Sumerian clay tablets discovered throughout the years, there are certain ancient texts that many believe are the ultimate evidence of advanced alien civilizations interacting with Early humans.
Without a doubt, one of the most controversial puzzles of mainstream archaeology is the sheer number of cuneiform tablets...
Mankind Survived A ‘Civilization Changing’ Extraterrestrial Impact 12,800 Years Ago
In a massive study that included 24 researchers and published in two scientific papers, experts found that our planet suffered the impact of a space object as early as 12,800 years ago when humans were already sedentary and were beginning to form the very first complex societies around the...
The ancient Egyptians may have used infrasound to create altered states of consciousness in...
YouTube Video Here: https://www.youtube.com/embed/gL6jwZNtVVk?feature=oembed&enablejsapi=1
The Egyptian pyramids are miracles of construction and scientific achievement, which is even more amazing when you consider that they were built thousands of years ago, long before we had the extensive knowledge that has been acquired over centuries.
But were the pyramids also constructed to produce...
30 Images That Prove The End Is Near
Because sometimes we, as a society need help to realize what exactly is going on around us, and how things have changed, and not for the better, here are 30 images that prove the end is near.
Take a look at the largest diamond mine in the world. The Mir...
These Are The 10 Avatars Of Vishnu, One Of The Main Ancient Hindu Deities
Lord Vishnu is one of the principal Hindu deities. It is said he appeared many times on the Earth plane as a physical incarnation (known in Hinduism as an Avatar). Vishnu is said to manifest a portion of himself upon the Earth whenever evil pervades. One of his major...
On the Trail of Alien Technology: Could Objects Like the “Aiud Wedge” Hold the...
In recent years, scientists have increasingly turned their attention to the possibility of finding evidence of extraterrestrial technology. This is partly due to the discovery of the first interstellar object known to have passed through our solar system, 'Oumuamua, which caused great excitement among astronomers and the public alike.
Interstellar...
Trending
cleopatra
How did Cleopatra die?
Cleopatra VII the queen of Egypt and one of the most famous women in history. Cleopatra rules over the prosperous Egyptian empire. She is beautiful, intelligent, and a master of manipulation. Every man she meets falls in love with her, including Julius Caesar and Mark Antony.
Over time, Cleopatra's ambitions...
Who was Cleopatra
When we hear the name Cleopatra, we think of a beautiful and alluring woman with a tragic story. But who was she? Cleopatra was the last active pharaoh of Ptolemaic Egypt and briefly survived as pharaoh by her son Caesarion. After her reign, Egypt became a province of the...
What did cleopatra look like?
Cleopatra, the Queen of Egypt, was one of the most renowned figures of her time. She was a beautiful, intelligent, and charismatic personality that used her power and influence to shape the course of history. However, her appearance and looks are still a mystery to the world as there...
News
LATEST ARTICLES
Did the Smithsonian cover up an Ancient Egyptian Colony in the Grand Canyon?
Did the Smithsonian Institute cover up the mind-boggling discovery of an ancient Egyptian Colony in the Grand Canyon? According to a news article from 1909, the answer is YES.
Is it possible that the ancient Egyptian civilization developed technology to travel across the planet? I'm not talking spaceships, but transoceanic voyages...
A massive, 200-million-year-old Footprint proves Giants existed?
YouTube Video Here: https://www.youtube.com/embed/dRuxw-nZoJw?feature=oembed&enablejsapi=1
Does this massive footprint left behind on a granite block which dates back at least 200 Million years prove giants were real? If it's not a footprint as skeptics suggest, then what else could it be?
South African Indiana Jones Michael Tellinger has made quite a few...
The Anunnaki Speak: A Message to Earth
"We have left you certain landmarks, placed carefully in different parts of the globe, but most prominently in Egypt where we established our headquarters upon the occasion of our last overt, or, as you would say public appearance. At that time the foundations of your present civilization were ‘laid...
Massive temple spotted on Mars ‘identical’ to an ancient Japanese tomb
According to satellite images from the red planet, there is a massive temple on Mars that is 'identical' to an ancient Japanese tomb.
There are some truly fascinating things on Mars. A baffling structure located on the surface of Mars eerily resembles a massive temple on Earth, and UFO hunters...
Mohenjo-Daro: An ancient city destroyed by a nuclear attack thousands of years ago?
Is it possible that Mohenjo-Daro - an ancient city that belonged to the Indus Valley Civilization- was destroyed by a nuclear attack thousands of years ago?
Only seven years after the first atomic explosion in New Mexico, theoretical physicist Robert Oppenheimer, one of the people often named as "father of...
Napoleon Bonaparte’s mystical experience inside the Great Pyramid of Giza
Did you know that Napoleon Bonaparte had a mystical experience inside the Great Pyramid of Giza? When a few of his most trusted men asked Napoleon what had happened inside of the Pyramid, Napoleon replied: ‘Even If I told you, you would not believe me.'
It is said that one night...
Inside Noah’s Ark: Suppressed video shows what was found inside
Do you believe the Great Flood really existed? What about Noah and the Ark? Well, according to many ancient texts and a fascinating VIDEO, the great Deluge did happen, and Noah's ark is real. This suppressed video even shows what's inside.
Scroll down for video.
Noah’s Ark and the Great Flood...
Videos that claim to show lifelike Anunnaki mummies ‘in stasis’ and artifacts found in...
YouTube Video Here: https://www.youtube.com/embed/JHOjSTbg9mY?feature=oembed&enablejsapi=1
What better way to prove the Anunnaki are not just a myth than to show an actual Anunnaki 'God'. Well, according to TWO videos uploaded to YouTube, not only were the Anunnaki real, governments around the globe recovered ancient alien technology and 'mummified' bodies of the...
Anomaly on Mars: Traces of a lost Martian Civilization?
The new image taken on SOL 1448 by the Curiosity Rover's MASTCAM shows a strange object with defined corners and straight lines, half buried in the ground. Is this the ultimate evidence of artificial structures on Mars as some suggest?
In the last couple of years, we have learned so...
Alien artifacts from ancient Egypt found in Jerusalem & kept secret by Rockefeller Museum
YouTube Video Here: https://www.youtube.com/embed/QwPTcmCb_KA?feature=oembed&enablejsapi=1
Alien enthusiasts have been left fascinated by reports of ancient Egyptian artifacts that were discovered in the home of famous Egyptologist Sir William Petrie. The artifacts are believed to be the ultimate proof of alien contact and are said to rewrite not only Ancient Egyptian history but...